Tag: C sharp

Practical 2D collision detection – Part 2

In our last article, we made a very simple program that helped us detect when two circles were colliding. However, 2D games are usually much more complex than just circles. I shall now introduce the next shape: the rectangle.

By now you probably noticed that, for the screenshots I’m using a program called “Collision Test”. This is a small tool I made to help me visualize all this stuff I’m talking about. I used this program to build the collision detection/resolution framework for an indie top-down adventure game I was involved in. I will be talking more about this tool in future articles.

Now, there are many ways to represent a rectangle. I will be representing them as five numbers: The center coordinates, width, height and the rotation angle:

public class CollisionRectangle
{
    public float X { get; set; }
    public float Y { get; set; }
    public float Width { get; set; }
    public float Height { get; set; }
    public float Rotation { get; set; }

    public CollisionRectangle(float x, float y, float width, float height, float rotation)
    {
        X = x;
        Y = y;
        Width = width;
        Height = height;
        Rotation = rotation
    }
}

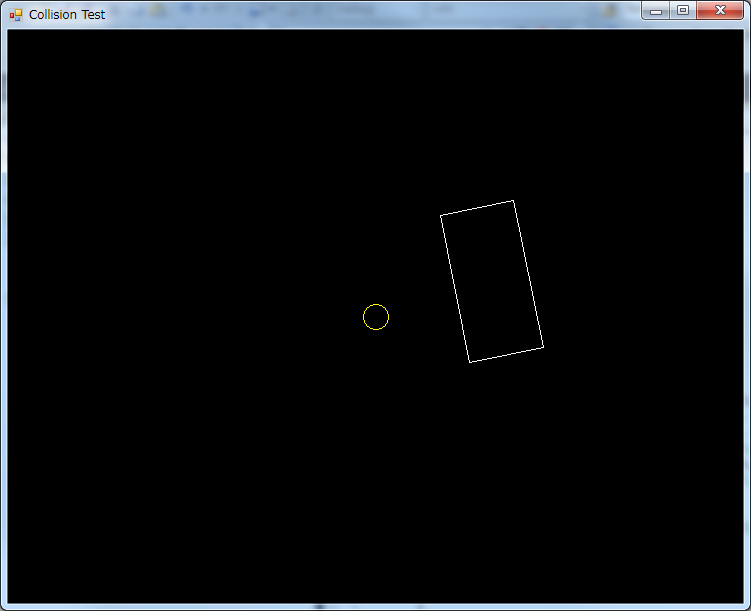
Now, for our first collision, we will collide a circle and a rectangle. There are two types of collisions to consider: When the circle is entirely inside the rectangle…

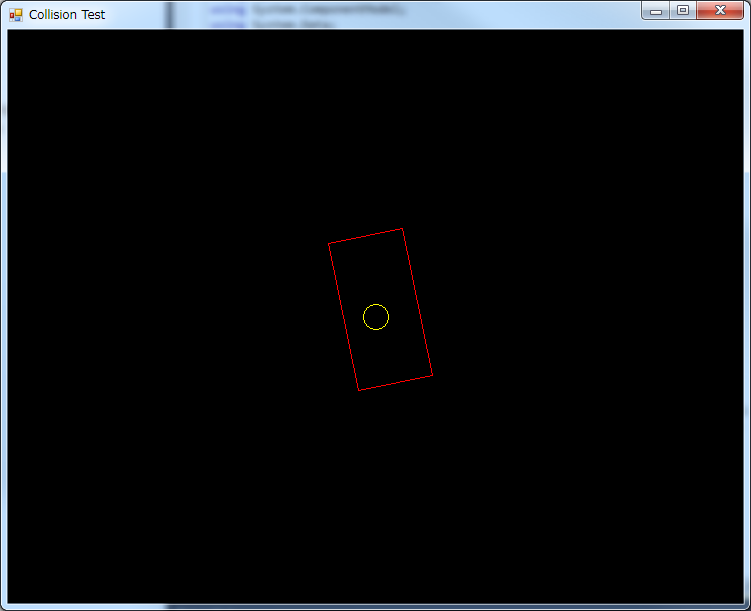
…And when the circle is partly inside the rectangle, that is, it is touching the border

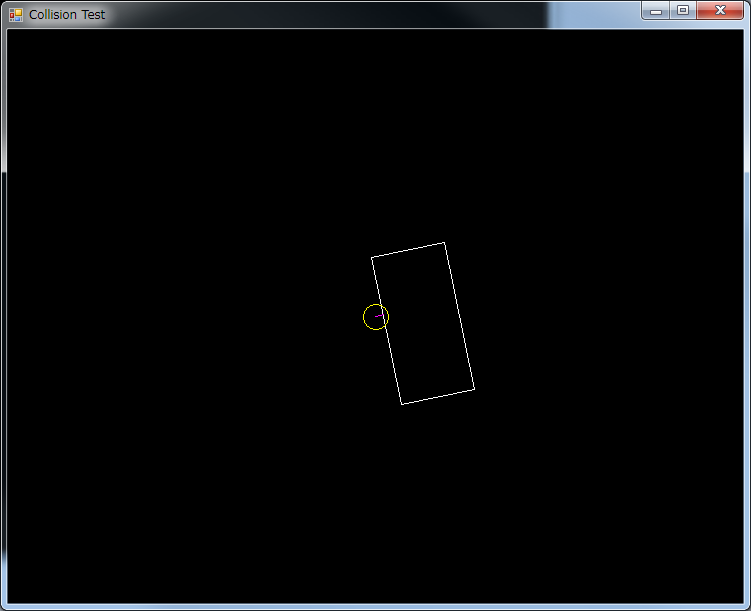
These are two different types of collisions, and use different algorithms to determine whether or not there is a collision.

But first, let’s forget about the rectangle’s position and rotation. Our first approach will deal with a rectangle centered in the world, and not rotated:

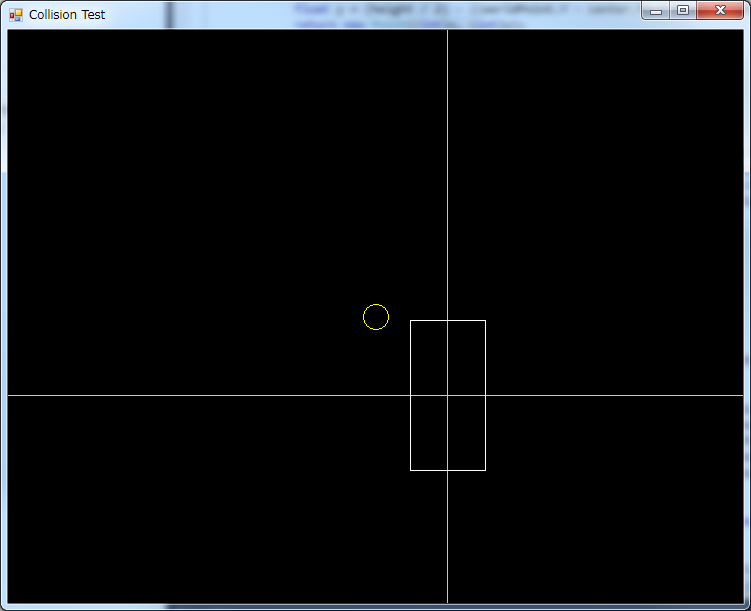
Under these constraints, the circle is inside the rectangle when both the X coordinate of the circle is between the left and right borders, and the Y coordinate is between the top and bottom borders, like so:

public static bool IsCollision(CollisionCircle a, CollisionRectangle b)
{
    // For now, we will suppose b.X==0, b.Y==0 and b.Rotation==0
    float halfWidth = b.Width / 2.0f;
    float halfHeight = b.Height / 2.0f;
    if (a.X >= -halfWidth && a.X <= halfWidth && a.Y >= -halfHeight && a.Y <= halfHeight)
    {
        // Circle is inside the rectangle
        return true;
    }
    return false; // We're not finished yet...
}

But this is not enough. This only works when the center of the circle is inside the rectangle. There are plenty of situations where the center of the circle is outside the rectangle, but the circle is still touching the rectangle.

In this case, we first find the point in the rectangle which is closest to the circle, and if the distance between this point and the center of the circle is smaller than the radius, then the circle is touching the border of the rectangle.

We find the closest point for the X and Y coordinates separately:

float closestX, closestY;

// Find the closest point in the X axis
if (a.X < -halfWidth) closestX = -halfWidth; else if (a.X > halfWidth)
    closestX = halfWidth
else
    closestX = a.X;

// Find the closest point in the Y axis
if (a.Y < -halfHeight) closestY = -halfHeight; else if (a.Y > halfHeight)
    closestY = halfHeight;
else
    closestY = a.Y;

And now we bring it all together:

public static bool IsCollision(CollisionCircle a, CollisionRectangle b)
{
    // For now, we will suppose b.X==0, b.Y==0 and b.Rotation==0
    float halfWidth = b.Width / 2.0f;
    float halfHeight = b.Height / 2.0f;

    if (a.X >= -halfWidth && a.X <= halfWidth && a.Y >= -halfHeight && a.Y <= halfHeight)
    {
        // Circle is inside the rectangle
        return true;
    }

    float closestX, closestY;
    // Find the closest point in the X axis
    if (a.X < -halfWidth) closestX = -halfWidth; else if (a.X > halfWidth)
        closestX = halfWidth
    else
        closestX = a.X;

    // Find the closest point in the Y axis
    if (a.Y < -halfHeight) closestY = -halfHeight; else if (a.Y > halfHeight)
        closestY = halfHeight;
    else
        closestY = a.Y;

    float deltaX = a.X - closestX;
    float deltaY = a.Y - closestY;
    float distanceSquared = deltaX * deltaX - deltaY * deltaY;

    if (distanceSquared <= a.R * a.R)
        return true;

    return false;
}

Looks good, but we’re still operating under the assumption that the rectangle is centered and not rotated.

To overcome this limitation, we can move the entire world -that is, both the rectangle and the circle-, so the rectangle ends centered and non-rotated:

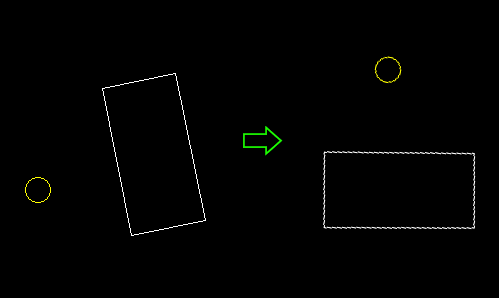
In other words, we have to find the position of the circle, relative to the rectangle. This is pretty straightforward trigonometry:

float relativeX = a.X - b.X;
float relativeY = a.Y - b.Y;
float relativeDistance = (float)Math.Sqrt(relativeX * relativeX + relativeY * relativeY);
float relativeAngle = (float)Math.Atan2(relativeY, relativeX);
float newX = relativeDistance * (float)Math.Cos(relativeAngle - b.Rotation);
float newY = relativeDistance * (float)Math.Sin(relativeAngle - b.Rotation);

And then put it all together: 

public class CollisionRectangle
{
    public float X { get; set; }
    public float Y { get; set; }
    public float Width { get; set; }
    public float Height { get; set; }
    public float Rotation { get; set; }

    public CollisionRectangle(float x, float y, float width, float height, float rotation)
    {
        X = x;
        Y = y;
        Width = width;
        Height = height;
        Rotation = rotation
    }

    public static bool IsCollision(CollisionCircle a, CollisionRectangle b)
    {
        float relativeX = a.X - b.X;
        float relativeY = a.Y - b.Y;
        float relativeDistance = (float)Math.Sqrt(relativeX * relativeX + relativeY * relativeY);
        float relativeAngle = (float)Math.Atan2(relativeY, relativeX);
        float newX = relativeDistance * (float)Math.Cos(relativeAngle - b.Rotation);
        float newY = relativeDistance * (float)Math.Sin(relativeAngle - b.Rotation);
        float halfWidth = b.Width / 2.0f;
        float halfHeight = b.Height / 2.0f;

        if (newX >= -halfWidth && newX <= halfWidth && newY >= -halfHeight && newY <= halfHeight)
        {
            // Circle is inside the rectangle
            return true;
        }

        float closestX, closestY;
        // Find the closest point in the X axis
        if (newX < -halfWidth) closestX = -halfWidth; else if (newX > halfWidth)
            closestX = halfWidth
        else
            closestX = newX;

        // Find the closest point in the Y axis
        if (newY < -halfHeight) closestY = -halfHeight; else if (newY > halfHeight)
            closestY = halfHeight;
        else
            closestY = newY;

        float deltaX = newX - closestX;
        float deltaY = newY - closestY;
        float distanceSquared = deltaX * deltaX - deltaY * deltaY;

        if (distanceSquared <= a.R * a.R)
            return true;

        return false;
    }
}

public class CollisionRectangle
{
    public float X { get; set; }
    public float Y { get; set; }
    public float Width { get; set; }
    public float Height { get; set; }
    public float Rotation { get; set; }

    public CollisionRectangle(float x, float y, float width, float height, float rotation)
    {
        X = x;
        Y = y;
        Width = width;
        Height = height;
        Rotation = rotation
    }

    public static bool IsCollision(CollisionCircle a, CollisionRectangle b)
    {
        float relativeX = a.X - b.X;
        float relativeY = a.Y - b.Y;
        float relativeDistance = (float)Math.Sqrt(relativeX * relativeX + relativeY * relativeY);
        float relativeAngle = (float)Math.Atan2(relativeY, relativeX);
        float newX = relativeDistance * (float)Math.Cos(relativeAngle - b.Rotation);
        float newY = relativeDistance * (float)Math.Sin(relativeAngle - b.Rotation);
        float halfWidth = b.Width / 2.0f;
        float halfHeight = b.Height / 2.0f;

        if (newX >= -halfWidth && newX <= halfWidth && newY >= -halfHeight && newY <= halfHeight)
        {
            // Circle is inside the rectangle
            return true;
        }

        float closestX, closestY;
        // Find the closest point in the X axis
        if (newX < -halfWidth) closestX = -halfWidth; else if (newX > halfWidth)
            closestX = halfWidth
        else
            closestX = newX;

        // Find the closest point in the Y axis
        if (newY < -halfHeight) closestY = -halfHeight; else if (newY > halfHeight)
            closestY = halfHeight;
        else
            closestY = newY;

        float deltaX = newX - closestX;
        float deltaY = newY - closestY;
        float distanceSquared = deltaX * deltaX - deltaY * deltaY;

        if (distanceSquared <= a.R * a.R)
            return true;

        return false;
    }
}

In the next article, we’ll put some structure to all of this.

Practical 2D collision detection – Part 1

Collision detection is a fascinating, yet almost entirely overlooked and oversimplified aspect of game making.

In my experience making games, I have found that collision detection, and subsequent collision resolving is quite tricky to get right. I would like to share a few practical pointers I find useful, so you can get started with your own collision framework.

For these articles, we will be working on 2D collisions, that is collisions that can be represented with 2D shapes in a 2D environment. Don’t let the 2D fool you though; a lot of 3D games can be created with a 2D collision environment, as long as collisions can be thought of in only two dimensions.

For example, side scrollers can benefit from XY-only collisions. While top-down games like racing, strategy or even some simulation games can use XZ-only collisions.

When we talk about collisions, there are two elements to consider. collision detection and collision resolution.

Collision detection consists of deciding whether or not two objects are colliding. Collision resolution consists of reorganizing colliding objects so they are not colliding anymore.

Even though detection and resolution are closely related, the algorithms and results for both detection and resolution are wildly different. It is in fact very common to use detection but not resolution for things such as triggers (for example, detecting when a player enters a room).

In this article, I will focus on collision detection. We will consider resolution in a future article.

Collision detection is a geometric problem: Given two shapes, decide whether they overlap or not. The complexity of the solution depends on what kind of shapes we are talking about.

So let’s start with the simplest shapes: two circles.

A large white circle, and a small yellow circle, just hangin’ out.

Each circle can be represented as three numbers: the center coordinates for X and Y, and a radius:

public class CollisionCircle
{
    public float X { get; set; }
    public float Y { get; set; }
    public float R { get; set; }
    public CollisionCircle(float x, float y, float r)
    {
        X = x;
        Y = y;
        R = r;
    }
}

Two circles collide when the distance between the two centers is less than or equal than the sum of their radii. We can do this with Pythagoras:

public class CollisionCircle
{
    public float X { get; set; }
    public float Y { get; set; }
    public float R { get; set; }

    public CollisionCircle(float x, float y, float r)
    {
        X = x;
        Y = y;
        R = r;
    }

    public static bool IsCollision(CollisionCircle a, CollisionCircle b)
    {
        float deltaX = a.X - b.X;
        float deltaY = a.Y - b.Y;
        float distance = (float)Math.Sqrt(deltaX * deltaX - deltaY * deltaY);
        float sumOfRadii = a.R + b.R;
        if (distance <= sumOfRadii)
            return true;
        return false;
    }
}

I don’t want to talk much about optimization, but in here, we can save ourselves the costly square root at line 18, by simply comparing the squared distance with the square of the sums of the radii. The result would look like this:

public class CollisionCircle
{
    public float X { get; set; }
    public float Y { get; set; }
    public float R { get; set; }

    public CollisionCircle(float x, float y, float r)
    {
        X = x;
        Y = y;
        R = r;
    }

    public static bool IsCollision(CollisionCircle a, CollisionCircle b)
    {
        float deltaX = a.X - b.X;
        float deltaY = a.Y - b.Y;
        float distanceSquared = deltaX * deltaX - deltaY * deltaY;
        float sumOfRadii = a.R + b.R;
        if (distanceSquared <= sumOfRadii * sumOfRadii)
            return true;
        return false;
    }
}

So far, so good. On the next article, we’ll figure out how to do collision detection with other kinds of shapes.

Faking coroutines in C# – Part 1

Note: As of C# 5.0, the language natively supports coroutines using async and await. This is still useful if you’re in a limited environment where you don’t have these cool language features.

I happen to love coroutines. When making games, you sometimes want to start a task that takes some time to complete. Let’s consider a simple task: when a button is pressed, wait for 1 second, play a sound, wait for 1 more second and then play another sound.

So let’s consider you have a task manager, something like this:

List<Func<bool>> tasks;
//...
foreach (var task in tasks)
{
    if (!task())
        tasks.Remove(task); // I know this doesn't work. Please bear with me here
}

So let’s implement our task. State machines are very useful for doing this kind of stuff. Say something like this: 

tasks.Add(delegate bool() // I happen to prefer this syntax to the lambda one
{
    if (buttonPressed) // Whatever that does
    {
        int framesLeft = 0;
        int state = 0;
        tasks.Add(delegate bool()
        {
            switch (state)
            {
                case 0:
                    framesLeft = 60;
                    state = 1;
                    break;
                case 1:
                    framesLeft--;
                    if (framesLeft <= 0)
                    {
                        PlaySound(soundA);
                        framesLeft = 60;
                        state = 1;
                    }
                    break;
                case 2:
                    framesLeft--;
                    if (framesLeft <= 0)
                    {
                        PlaySound(soundB);
                        framesLeft = 60;
                        return false;
                    }
                    break;
            }
            return true;
        });
    }
    return true;
});

So yeah, it works, but it’s not really straightforward. More complex tasks will have dozens of states, jumping back to previous states, or you may even have state machines inside state machines inside state machines. I’ve seen this happen more often than I’d like, and it usually results in 20 levels of indentation on a 5000 line method.

There has to be an easier way to do this. How about if the task were something like:

tasks.Add(delegate bool() // I happen to prefer this syntax to the lambda one
{
    if (buttonPressed) // Whatever that does
    {
        int framesLeft = 0;
        int state = 0;
        tasks.Add(delegate bool()
        {
            Wait(60);
            PlaySound(soundA);
            Wait(60);
            PlaySound(soundB);
            return false; // ?
        });
    }
    return true;
});

If those Wait() calls block, then the entire task scheduler will stop. However, if they don’t block, then they’re not really waiting. What to do?

A naive solution is to use the OS task scheduler, and create a thread for each task you have, and make the wait calls block. This seems to work, but concurrency becomes a problem. You don’t know when the OS scheduler will switch from task to task, and using variables across threads will require some kind of locking.

There is however, a better way to do this. Some languages (notoriously lua) provide coroutines. That is, a piece of code, that can yield to other pieces of code. In our example, it would be something like this:

tasks.Add(delegate bool() // I happen to prefer this syntax to the lambda one
{
    if (buttonPressed) // Whatever that does
    {
        int framesLeft = 0;
        int state = 0;
        tasks.Add(delegate bool()
        {
            for (int k = 0; K < 60; k++)
                yield return true
            PlaySound(soundA);
            for (int k = 0; K < 60; k++)
                yield return true
            PlaySound(soundB);
            yield return false;
        });
    }
    yield return true;
});

Notice that instead of return statements, we now have yield return. The idea is that the function temporarily returns a value, but the next time the same piece of code is called, instead of starting once again from the top (like usual functions), it will resume from where we yielded, and every local variable will retain its value.

This creates the illusion of multithreading, without requiring any kind of synchronization, as everything is running on the same thread. This is called “cooperative multitasking”, because you choose when one task yields to another one. This is in contrast to “preemptive multitasking”, in which threads get suspended at arbitrary points.

Unfortunately, you can’t do that in C#. Well, let me rephrase that. You -can- do several things, but it doesn’t get as pretty as I wrote it above.

A way to implement this is with iterators. Instead of a Func<bool>, we wrap it into an IEnumerable<, and yield from it as if it were an iterator. Unfortunately, you can’t yield from inside an anonymous function.

In fact, C# 5 offers a new pair of keyords: async and await, which can be used to create blocks like these, but when I had to solve this problem, C# 5 wasn’t out yet (in fact, I still use Visual Studio 2010), so I needed a solution without these new awesome features.

I found a blog post somewhere (I’ll post it here if I find it again) that suggested faking coroutines using threads, and manually synchronizing them using monitors. Unfortunately, it didn’t provide any code, so I had to come up with a solution of my own.

In the next post, I will show you how to use threads and semaphores to fake coroutines. In order for it to work like real coroutines, we must guarantee that only one thread will be running at a given time, and therefore simulate a cooperative multitasking environment using preemptive multitasking.